The Law of Small Numbers

Daniel Kahneman, a celebrated psychologist, and Nobel laureate, introduced a fascinating concept: the "law of small numbers." But what is it exactly? And why should we care?

Let's start from the basics, the "law of large numbers." Imagine a massive sack filled with UK coins of different denominations - 1, 2, 5, and 10 pennies. Picture countless people taking turns, each drawing one coin. The law of large numbers suggests that, over time, the average amount people pocket will gradually approximate to 4.5 pennies, the mean value of all denominations.

But what about the law of small numbers? The theory would hold true if the first few coin drawers averaged out to 4.5 pennies. Yet, this is unlikely. The first few might all draw a 10-penny coin. Therefore, unlike its big brother, the law of small numbers falls flat.

Remember, these terms are metaphoric, not literal. They apply beyond coin-tossing scenarios. For instance, in research, smaller samples reflect the overall population less accurately. Conversely, larger samples provide a more representative picture. If you rush to conclusions from a tiny sample, you're essentially agreeing with the law of small numbers, a fallacy.

Let's illustrate this with a real-life example. Say a girl dated three men, and all turned out to be unpleasant. She concludes that all men are the same - a premature generalization. She believes her small sample size is representative of all men, a classic sign of trusting the law of small numbers.

This belief also links to what Kahneman coined as the "representativeness heuristic."

Think of Freud formulating the principles of psychoanalysis based on just seven patients. Or consider common stereotypes like all BMW drivers never signal and many others of that kind. All these illustrate the pervasive influence of the law of small numbers.

Have you ever wondered how e-commerce marketing relates to this? Many business owners commonly assess website performance based on a short 1-2 day timeframe.

Take an example from this picture:

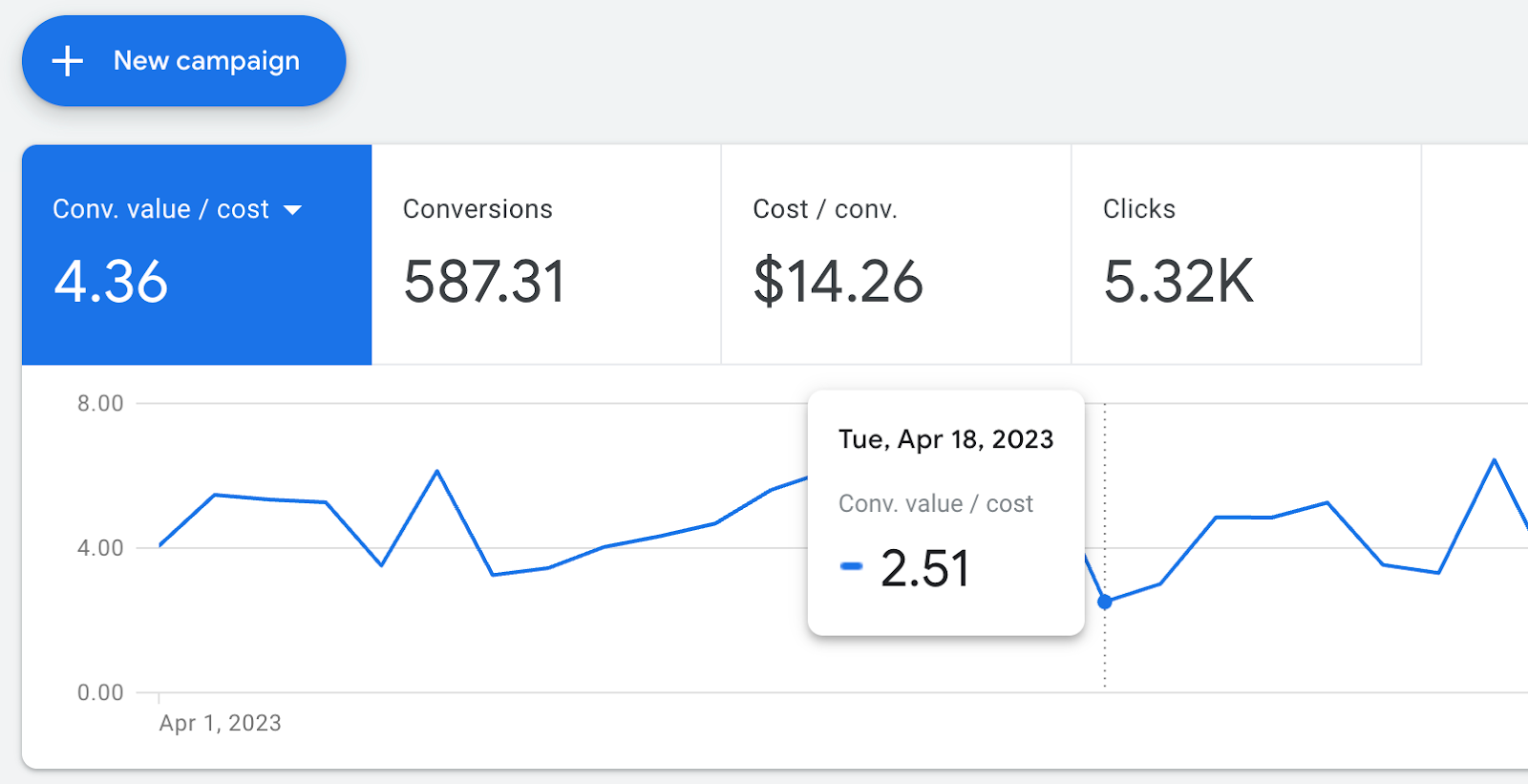
The average return on ad spend (ROAS) over a 30-day period is 4.36. However, if you examine it on a daily basis, you'll notice consistent fluctuations in ROAS. On Monday, it's 5.94, then on Tuesday, it drops to 2.51, but it bounces back on Wednesday. That's why evaluating Google or Facebook campaigns, as well as any Google Analytics reports, for just one day is rather pointless unless something highly specific occurred on that particular day.

A great example from the film "The State Counseller" shows a character expecting a uniform alternation of red and black playing cards, thus demonstrating the law of large numbers, after just three draws. This, again, signifies belief in the law of small numbers and a cognitive bias known as the "gambler's fallacy."

The law of small numbers also pervades pseudosciences, where it's used to over-generalize and misrepresent people and phenomena.

In sum, our tendency to believe in the law of small numbers is a common cognitive bias. During rigorous scientific research, however, it can be debunked with the right statistical methods and sample sizes. So, the next time you wonder if an occurrence is likely or accidental, remember to question your assumptions and examine your sample size. Don't let the law of small numbers fool you.